Двумерная свертка в этих обозначениях может быть записана или как одномерная свертка многочленов,

s.(</) = Е gi--kiy)df{y). ИЛИ как произведение многочленов от двух переменных, S {X, y)=g (X, у) d (X, у).

Двумерная циклическая свертка также может 6бгть выписана в терминах многочленов, а именно,

S (х, у) g {X, у) d {х, у) (mod х ~ 1) (mod - 1), где я не обязательно равно я . Для двумерной циклической свертки выполняется теорема о свертке. Если D и G обозначают двумерные преобразования Фурье таблиц d и g соответственно и Sk-,k = Gk.k-Dk.k; то S является двумерным преобразованием Фурье таблицы s. Следовательно, для вычисления двумерной циклической свертки можно пользоваться двумерным БПФ-алгоритмом. Можно, конечно, пользоваться и прямыми методами вычисления двумерных сверток.

Имеется много способов прямого вычисления двумерной линейной и.ти циклической свертки. Простейший путь состоит в том, чтобы попытаться вычислить ее как последовательность одномерных сверток сначала по строкам, а зате.м по столбцам. Заметим, однако, что в формуле

. W-l -N -1

Sc, i> = и S gl-k-. l--k dk, к

k=0 I 4--0

выделенная в квадратные скобки линейная свертка по k должна быть вычислена для всех i и к.

Понять двумерную свертку легче, если выписать ее в виде свертки многочленов,

Si{y)=gf-k-{!/)dk-{y) <=0..... L + N-2.

Из этой формулы ясно видна реализация двумерной свертки как LN произведений многочленов, каждое из которых, в свою очередь, является сверткой, требующей L N умножений. Всего, таким образом, получаем LCNN умножений, что, конечно, недопустимо для больших задач, так что нужны быстрые алгоритмы.

Хотя рассмотренные в гл. 3 алгоритмы свертки строились над полями, они на самом деле выполнимы и в некоторых кольцах, в частности, в кольце многочленов. Следовательно, свертка много-

членов может быть вычислена любым из этих быстрых алгоритмов. Стожение в этих алгоритмах становится сложением многочленов, а умножение - умножением многочленов. Эти последние умножения, в свою очередь, являются свертками и могут быть вычислены с помощью быстрых алгоритмов свертки. Таким образом, мы получаем способ вычисления двумерной свертки, состоящий во включении одного быстрого алгоритма одномерной свертки в другой быстрый алгоритм одномерной свертки.

Все сказанное здесь относительно линейной свертки, конечно, относится и к циклической свертке и к вычислению произведения многочленов по модулю многочлена т {х).

Например, для вычисления двумерной циклической (4X4)-свертки воспользуемся алгоритмом 4-точечной циклической свертки в виде, представленном на рис. 3.14: s = С [(Bg)-(Ad)]. Этот алгоритм содержит пять умножений и 15 сложений. Следовательно, применение его для циклической свертки многочленов потребует пяти умножений многочленов и 15 сложений многочленов. Каждое умножение многочленов само является сверткой, и, следовательно, для его вычисления по этому алгоритму потребуется пять вещественных умножений и 15 вещественных сложений. Таким образом, для вычисления двумерной циклической (4х4)-свертки потребуется в данном алгоритме 25 вещественных умножений и 135 вещественных сложений. Эта процедура представлена на рис. 7.1 для вычисления циклической (пхп )-свертки. Как показано на рисунке, подпрограмма должна знать индекс к и иметь доступ к заранее вычисленной таблице Gt-t-.

Используя последовательные операции над двумерными таблицами, этот составной алгоритм можно представить в виде единого алгоритма. Сначала умножим строку таблицы d на матрицу А , а каждую строку таблицы g на матрицу В . Затем умножим каждый столбец первой новой таблицы на А и каждый столбец второй новой таблицы на В. Это даст нам две таблицы размера М {п)У. М {п. ). Перемножим покомпонентно эти таблицы. Полученную таким образом(Ai {п)хМ (я ))-таблицу преобразуем к нужной выходной таблице s размера п X п , умножив сначала каждый ее столбец на С, а затем каждую строку полученной таблицы на С.

На рлс. 7.2 для сравнения выписаны эта процедура и процедура, основанная на двумерном преобразовании Фурье и теореме о свертке. Ясно, что рассматриваемая процедура является обобщением процедуры, основанной на двумерном преобразовании Фурье. Теперь преобразование состоит только из сложений, но размер промежуточной таблицы равен не пХп , а М {п)х кМ (и ).

Гнездовой алгоритм является более общим и в другом отношении: он позволяет вычислять двумерное произведение много-

Ввод вектора многочленов

Ввод вектора d коэффицие нтов многочлена д(х) = DAx)

Сложение многочленов

s(jr) = C S(A-)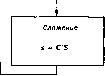

Выход

Рис. 7.1, Алгоритм двумерной циклической свертки.

членов по модулю любых многочленов т (х) и т (г/), а метод, основанный на преобразовании Фурье, позволяет вычислять произведение только по модулю X - 1 и у - 1.

Характеристики гнездового алгоритма задаются числом М (п X X я ) необходимых умножений и числом Л (пхп ) необходимых сложений. Легко видеть, что полное число умножений равно

М {пхп ) = М ( ) М (п ). Аналогично, из рис. 7.1 легко увидеть, что

А (пхп ) = пА (п ) + М {п ) А ( ).

Полное число умножений не зависит от того, какой из делителей назван я, а какой п . Но число сложений зависит от такого выбора, и поэтому необходимо просматривать оба варианта. На-

Вход

в двумерную свёртку в частотной области

Вход

i гнездовой алгоритм свертки Винограда

Преобразование Фурье каждой строки матриц dug

Затем преобразование Фурье каждого сполбца

w - [ ].

-Умножить каждую строку матрицы ii на К и каждую строку матрицы g иа В

Затем умножить каждый столбец новых таблиц на К и о соответственно где матрицы А,А ,Ви В содержат только О и ±1

-Обратное

преобразование Фурье каждой строки таблицы S Обратное

преобразование Фурье каждого столбца

Выход

Умножить каждый столбец таблицы S на с

Затем умножить каждую строку новой таблицы на С

Выход

свертка (mod х * - 1) (mod У - 1)

Сверт

(mod ш-( у))

Рис. 7,2. Сравнение способов вычисления двумерной свертки.

пример, двумерную цик.таческую (7х9)-свертку можно вычислять с помощью одномерных алгоритмов с характеристиками

М (7) = 16, А (7) = 70,

М (9) = 19, А (9) = 74.

Полное число умножений при это.ч равно 304, а полное число сложений равно 1848 или 1814 в зависимости от того, чему выбрано равным п.

п-1 *-0

1=0, .... Л - 1,

где двойные скобки в индексах обозначают вычисление по модулю п.

Мы хотим преобразовать одномерную свертку в двумерную. Для этого воспользуемся китайской теоремой об остатках, позво-

Лвумернап \ циклическая 0 . свертка

Ёо Si,

Рис. 7.3. Иллюстрация алгоритма Агарвала-Кули.

ляющей отобразить одномерный вектор входных данных в двумерную таблицу и выходную двумерную таблицу в одномерный вектор. Заменим индексы i и к парами индексов (( , Г) и (к, к ) по правилу

i = i (mod я), I = i (mod л ), к = к (mod л), к = к (mod л ). Занимаясь китайской теоремой об остатках, мы уже видели, что старые индексы восстанавливаются по новым согласно формулам

где целые числа Л и Л определяются равенством Nn + Nn = 1.

Это то же самое соответствие между компонентами вектора и компонентами двумерной таблицы, которое было использовано в алгоритме Гуда-Томаса. Описанное отображение иллюстрируется рис. 7.3. Свертку

можно записать в виде

8 -л-С-(-Л-п-Г

fe-O fe=0

r-)i-)d -n-*-(- -/i*--

7.2. Алгоритм Агарвала-Кули вычисления свертки

Алгоритм Агарвала-Кули представляет собой метод преобразования лrt -точечной одномерной циклической свертки в двумерную циклическую (пхп )-свертку при условии, что числа п и п взаимно просты. Его можно использовать для того, чтобы скомбинировать алгоритм Винограда вычисления л-точечной циклической свертки, содержащий М {п) умножений, с алгоритмом Винограда вычисления п-точечной циклической свертки, содержащим Af {л) умножений, и построить алгоритм вычисления -точечной циклической свертки, содержащий Ж ( ) М (л ) умножений.

В основе алгоритма Агарвала-Кули преобразования одномерной циклической свертки в многомерную циклическую свертку лежит китайская теорема об остатках для целых чисел. Этим алгоритм отличается от алгоритма Винограда, в котором используется китайская теорема об остатках для многочленов. Он не обеспечивает столь сильного уменьшения числа умножений, как алгоритм Винограда вычисления свертки, но, с другой стороны, он не имеет и тенденции к чрезмерному росту с ростом л числа сложений, как в алгоритме Винограда. Кроме того, он лучше структурирован. Если п велико, то алгоритм Агарвала-Кули более управляем, так как может быть разбит на подпрограммы. Для построения хороших алгоритмов свертки надо использовать алгоритм Агарвала-Кули разбиения длинной свертки на короткие циклические свертки, для вычисления которых использовать затем эффективные алгоритмы Винограда вычисления коротких циклических сверток.

Алгоритм Агарвала-Кули строится на трех идеях. Сначала одномерная циклическая свертка с помощью китайской теоремы об остатках (К. Т. О.) для целых чисел преобразуется в многомерную циклическую свертку; затем вдоль каждой координаты используется алгоритм Винограда вычисления короткой свертки; и, наконец, для сборки вместе полученных преобразований используется теорема о кронекеровском произведении для матриц.

Пусть заданы di и для t = О..... п - 1, и нам надо построить компоненты циклической свертки