Глава 6

ВЫЧИСЛЕНИЯ В СУРРОГАТНЫХ ПОЛЯХ

Часто задачу вычисления в заданном поле можно вложить в другое поле, произвести там необходимые вычисления, а затем ответ вернуть в заданное поле. Целесообразность такого перехода может мотивироваться различными причинами. Может оказаться, что в новом поле необходимые вычисления выполнить легче, и это уменьшает объем работ или упрощает реализацию вычислений. Иногда электронные компоненты для вычислений в некотором поле доступнее, чем для заданного поля, и тогда, если требуемые вычисления допускают подходящую переформулировку, резоннее перейти в эго поле. Возможны ситуации, когда желательно разработать стандартный вычислительный модуль обработки больших массивов данных и использовать его при решении разнообразных задач для обработки дискретных сигналов. Подгонка одного типа вычислений к другому может осуществляться тогда с целью стандартизации.

Другой важной причиной использования суррогатных полей является улучшение точности вычислений. Вычисления в полях Галуа не содержат погрешностей округления и поэтому всегда г точны. Если задачу вычисления в поле вещественных или комп- , лексных чисел удастся погрузить в поле Галуа, то это может при- j вести к увеличению точности результата. В большинстве задач,] обработки дискретных сигналов можно ограничиться вычисле- ниями с фиксированной запятой; обычно оказывается достаточной! 16-битовая арифметика с фиксированной запятой. Если поле! Галуа достаточно велико, чтобы содержать 16-битовые целые! числа, то в его пределах можно правильно осуществлять многие! целочисленные операции, если только результаты не выходят! за пределы 16-битовых целых чисел.

6.1. Свертка в суррогатных полях

Свертка в поле вещественных чисел часто может быть зам нена сверткой в подходящем поле Галуа. В реальных задача! вещественные числа записываются в виде конечного числа д& сятичных или двоичных знаков; в цифровой обработке сигнале

обычно используется запись с фиксированной запятой. Двоичное представление с конечным числом знаков может ограничиваться 12 или 16 битами. При вычислениях можно предполагать, что двоичная точка находится справа - все числа являются целыми. Сдвиг двоичной точки во входных данных с целью включения остальных случаев является очень простым делом. Итак, линейную свертку

S (X) = g (X) d (X)

в поле вещественных чисел мы заменяем сверткой в кольце целых чисел. Для этого нужно только входные данные интерпретировать как целые числа. Внешний вид уравнения, описывающего свертку, не меняется, но операции приобретают смысл стандартной целочисленной арифметики. Затем уравнение в кольце целых чисел можно погрузить в подходящее поле Галуа, скажем, простое поле Галуа, GF (р), если простое число р достаточно велико. Если все входящие в свертку целые числа положительны, то задающее простое поле GF (р) простое число р должнЬ быть столь большим, чтобы выходные коэффициенты свертки не превосходили р - 1. Тогда выполняется сравнение

S (хУ е (х) d (х) (modp),

и условие вычислений по модулю р излишне. Если Sj могут принимать и отрицательные значения, то задающее простое поле GF (р) простое число р надо выбирать так, чтобы Si попадали в диапазон - (р - 1)/2 < Sj < (р - 1)/2. Тогда отрицательные целые числа могут быть представлены положительными целыми числами в интервале от (р + 1)/2 до р - 1.

Свертка в поле Галуаможет быть вычислена любым из пригодных в данном поле методов. Некоторые прямые методы рассматриваются в следующем разделе. Можно также воспользоваться преобразованием Фурье в данном поле и теоремой о свертке. На рис. 6.1 приводится сравнение такого вычисления в поле Галуа и в поле комплексных чисел. Мы видим, что на обеих сторонах рисунка выписаны одинаковые уравнения, хотя, конечно, заложенные в них арифметики различны.

Так как циклическая свертка в поле Галуа приводит к тому же самому ответу, что и циклическая свертка в кольце целых чисел, то использование преобразования Фурье данного поля Галуа также приводит к правильному ответу. Так как арифметикой поля GF (р) является арифметика по модулю р, то переполнения по модулю р в промежуточных вычислениях роли не играют, но могут оказаться существенными в выходных вычислениях; если р выбрано достаточно большим, то переполнения в выходных данных невозможны.

1У4 1л. ь. Вычисления в суррогатных поляя

6.1. Свертка в суррогатных полях

Выиисление ивлоиислеиной сввргт

Процедура i: Вложение целых иисел 6 С ; арифметика поляС

Процедура 2: Вложение целых чисел в 6F(p),

арифметика поля 6F\P).

S. = 0,D,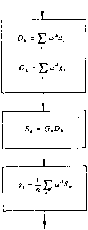

Рис.

six)

6.i. Сравнение двух процедур свертки.

six)

В качестве примера рассмотрим вычисление 5-точечной циклической свертки,

S W = g W d W (mod X - 1).

Выберем простое р равным 31 и будем работать в поле GF (31). Это по.те подходит к рассматриваемой задаче посто.чьку, поскольку нам известно, что коэффициенты свертки s (х) не превосходят 30. Для реально возникающих задач поле GF (31) слишком мало и мы его выбрали только для примера.

Так как 5 делит р - 1 = 30, то в данном поле существует преобразование Фурье длины 5. Ядром преобразования можно

выбрать элемент 2, так как его порядок равен 5. Пусть d = 2, rfi = 6, dj = 4, d3 = 4, d, = 0, go = 3, gi = 0,igj = 2, g, - 1, g4 = 2.

5-точечное преобразование вектора d задается равенствами

Оь= S2 (ii, А = 0, 4;

для вектора g имеют место аналогичные соотношения. В матричной записи соответственно имеем

D. О,

Таким образом, компоненты векторов-преобразований даются равенствами

Do = 16, Dj = 0, = 5, D, = 29, = 22,

G = 8, Gi = 20, Gj = 22, G3 = 0, Gj = 27.

Перемножая и Gj, для S, получаем;

S, = 4, S, = 0, = 17, S3 = 0, Sj = 5.

Так как 5-25 = 1 в поле GF (31), то = 25. Стедовательно, обратное преобразование Фурье задается равенством

определяющим окончательный результат. Непосредственное вычисление этой свертки в кольце целых чисел дает тот же результат. Если мы выберем большие входные компоненты, то некоторые компоненты свертки окажутся больше 30. В этом случае вычисление св.фтки в GF (31) приведет к переполнению выходных компонент и даст неправильный результат. Тогда нужно использовать большее поле; в практических приложениях полезны поля, содержащие по меньшей мере 2° элементов.

Если длина слова слишком велика для поля желаемой мощности, то можно воспользоваться китайской теоремой об остатках и работать с вычетами целых чисел, разбивая таким образом длинные слова на короткие подслова. Это использование китайской тео-

ремы об остатках отличается от ее предыдущего использования при построении переупорядочивания линейного потока данных в таблицу. Теперь она используется только для разбиения самих чисел, не затрагивая индексацию данных: данные следуют в своем естественном порядке. Новые свертки, конечно, можно вычислять, используя опять китайскую теорему об остатках, но на сей раз, в отличие от предыдущего, она будет использоваться для вновь сформированных многочленов и их индексов.

Пусть si обозначает вычет s, (mod mi) для г взаимно простых

целых чисел mi, mj..... m,. Тогда

-1 i = О.....L + N - I,

sl = (modm,).

1 = 0, ... , Г,

где gY = gi (mod mi) и = di (mod mi). По китайской теореме об остатках величины Sj восстанавливаются по вычетам sl -Следовательно, вычисление свертки, содержащей большие целые числа, мы свели к вычислению г сверток, содержащих малые целые числа. Для вычисления этих составляющих сверток можно пользоваться уже описанными способами или быстрыми алгоритмами вычисления сверток в кольце целых чисел.

6.2. Числовые преобразования Ферма

Простейший вид алгоритмы вычисления преобразования Фурье имеют в полях Галуа вида GF {2 + 1), которые действительно являются полями, если р = 2 -f 1 - простое число. Известно, что число 2 -Ь 1 не является простым, если т не равно степени двух. Однако обратное утверждение неверно, так как число 2 + 1 является составным. Но при m = 2, 4, 8 и 16 число 2 -f 1 является простым, равным соответственно 5, 17, 257 и 65 537. Это множество целых чисел известно под названием простых чисел Ферма. Если q - простое число Ферма, то в поле GF (q) число q - 1 и любой его делитель равны некоторой степени двойки. Преобразование Фурье

Vft = Ё * = 0.....п-1,

определено, если п делит 2 и существует элемент ш порядка п ). Таким образом, в поле GF (2 + 1) определены преобразования Фурье длин 2 , 2, 2 , 2 2. Используя алгоритм Кули- Тьюки, преобразование Фурье в поле GF (2 + 1) можно пред-

ставить в виде последовательности преобразований по основанию два. для реализации которой требуется всего лишь примерно (л/2) logs, п умножений и (я,2) log. п сложений.

Преобразования длины 32 и меньше в поле (2-f 1) делаются на самом деле намного проще. Это обусловлено тем, что порядок элемента 2 в этом поле равен 32. Чтобы увидеть это, достаточно заметить, что 2 -f 1 = О в поле GF {2 + 1). Следовательно, 2 = -1 и 2 = 1. Преобразование Фурье записывается в виде

Vs = Е 2 oi, к = 0.....31,

и умножение в данной арифметической системе сводится просто к циклическому сдвигу, так как представляет собой умножение на степени двойки. Такое преобразование вычисляется чрезвычайно просто, но длина 32 слишком мала для многих приложений.

В общем случае простого числа Ферма 2 + 1 порядок элемента 2 в поле GF (2 + 1) равен 2т, так что 2 может быть использовано в качестве ядра преобразования длины 2т. Для построения j]peo6pa30BaHHH Фурье длины 4т можно воспользоваться ядром > 2. В этих полях, как легко проверить возведением в квадрат и использованием соотношения 2 = -1, выполняется равенство у 2 = 2 (2 * - 1). Поэтому каждая степень элемента > 2 имеет вид 2 ± 2.

Например, преобразование Фурье длины 64 в поле GF (2 + 1) записывается в виде

k = Q, 63.

} Такое преобразование Фурье называют часто числовым преобразованием Ферма. - Прим. перев.

Если для этого вычисления воспользоваться БПФ-алгоритмом Кулн-Тьюки по основанию два, то все умножения на константы будут умножениями на чнсла вида 2 i 2* и, следовательно, могут быть реализованы как пара циклических сдвигов и вычитание. В общем случае поля GF {2 + 1) преобразование Фурье длины большей чем 2 всегда содержит нетривиальные умножения. Число этих умножений можно уменьшить сведением БПФ-алгоритма Кули-Тьюки в форму многомерного преобразования, в каждом из измерений которого используется не более чем 2т-точечное преобразование.

Например, рассмотрим !024-точечное преобразование в поле

{2 + п.

1023

= £ к = 0..... 1023,

где 0) - элемент порядка 1024, который можно полагать равным п , где л - примитивный элемент поля. Элемент 3 в поле