а длина выходного блока равна L ~\- N - 1; последовательность s называется выходной или сигнальной. В записи свертки подразумевается, что = О при ( - 4 < 0. Так как все компоненты последовательности g умножаются на все компоненты последовательности d, то прямой метод вычисления свертки содержит NL умножений.

Имеется очень разработанная теория построения КИО-фильт-ров, связанная с выбором длины L и весовых множителей \g,]. Этот аспект теории конструкций фильтров мы не рассматриваем; предметом наших исследований являются быстрые алгоритмы вычисления выходной последовательности s по заданным последовательностям фильтра g и входа d.

Со сверткой тесно связана еще одна величина, которая называется корреляцией и определяется равенствами

г, = И guA. 1=0, L + Af-2,

где gi+ji = О при ( Корреляцию можно вычислять как

свертку, если просто прочитать одну из определяющих ее последовательностей в обратном порядке. Все способы вычисления линейной свертки легко преобразуются в способы вычисления корреляции.

Свертку можно записать также через многочлены. Пусть d(x) = da и gW = Sgi-

Тогда , s(x) = g(x) d(x), где s(x) = цх. Эти равенства легко

проверяются простым вычислением коэффициентов произведения g{x)d{x). Можио, конечно, записать также равенство s (*) = =d{x)g(x),m которого становится очевидной симметричная роль последовательностей g и d в определении свертки. Таким образом, линейная свертка может быть записана в эквивалентном виде как

Si = S

Другой формой свертки, тесно связанной с линейной сверткой, является циклическая свертка. Для заданных двух последовательностей i = О, п - 1} и \gi, i = О..... п - 1( с

одной и той же длиной блока п циклическая свертка ]s, ( = О, л - 1} с длиной блока п определяется равенствами

Si = Б g((i- )4. i = 0.....1-1,

где двойные скобки означают, что вычисления над индексами производятся в арифметике по модулю п (см. разд. 2.6). Иными словами, ((п - k)) = п - k (mod n) и О < ((га - к)) < п. Заметим, что в циклической свертке при каждом i каждое d умножается на значимую величину gm-i))- Это существенное отличие от линейной свертки, в которой dj часто умножается на член gj.j, индекс которого выходит за диапазон определения последовательности g, так что соответствующая компонента равна нулю.

Циклическую свертку можно связать с линейной следующим образом. По определению циклической свертки

S( = S g((i-6))dft. = 0.....n-1.

Разделим эту сумму на две, выделяя в первую сумму члены, индексы которых удовлетворяют условию i - А > О (или & < i), а во вторую - члены, индексы которых удовлетворяют условию i - k <Ч (или к > i):

4=0 ft-i+l

Полагая теперь в первой сумме = О при i > (, а во второй gntt-h = О при к < I, можно изменить границы суммирования и получить связь циклической и линейной сверток в виде

Si = £ gi-A + Е gn+i-bdk = s, + s +i, 1 = 0,..., п - 1.

A=0 k=fl

Скажем, что члены последовательности s, индексы которых больше га - 1, вкладываются обратно в члены, индексы которых меньше п.

Если второй член выписанной выше суммы равен нулю, то линейную свертку можно вычислять как циклическую. Это возможно, если произведения gnti-hdh равны нулю для всех / и к. Чтобы обеспечить эти условия, можно так выбрать длину я циклической свертки, чтобы она была больше, чем N + L - 1 (пополняя нулями g и d до длины блока п). Тогда для вычисления линейной свертки можно пользоваться алгоритмом вычисления циклической свертки и получать при этом правильный ответ.

Циклическую свертку можно также выразить в виде произведения многочленов. Пусть

d (X) = Е diX. g (X) = Е giX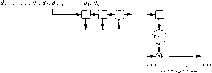

Выбрать средние т б нииестве кснррп иицлиескаС/ cSpmru

Рис. 1.6. Использование КИО-фильтра для формирования циклической свертки.

И S (х) = g (jc) d (х). Циклическая свертка вычисляется по многочлену S (д:) обратным вложением членов высшего порядка. Это можно представить в виде записи

s (х) = S {х) (mod X - 1), где равенство по модулю х - 1 означает, что s (х) равен остатку от деления многочлена s (х) на многочлен х - 1. Таким образом, s (X) =g(x)d (X) (mod x - 1).

Для приведения многочлена g (х) d (х) по модулю х - 1 достаточно заменить д: на 1, или, что эквивалентно, член x+ с положительным ( на член х. Это соответствует формированию величин

s, = s, + s + i = 0.....л - 1,

и, следовательно, позволяет вычислить коэффициенты циклической свертки. Так как

s (X) d{x)g (X) = g{x)d (X) (mod x - 1),

TO ясно, что векторы d и g играют в определении свертки симметричную роль, так что циклическая свертка задается двумя эквивалентными равенствами

si = Е gW-kn<i =

fi-I

= S i((( j,)gs, / = 0, n-1.

На рис. 1.6 приведена схема КИО-фильтра, вычисляющего циклическую свертку, для чего последовательность d повторяется дважды. На выходе КИО-фильтра формируется последовательность из Зп - 1 компонент, среди которых содержатся п последовательных компонент, равных компонентам циклической свертки.

Более важным для приложений является использование циклической свертки для вычисления длинной линейной свертки. В быстрых алгоритмах вычисления длинной линейной свертки входная последовательность разбивается на короткие секции, содержащие иногда несколько сотен отсчетов. Для формирования потока данных на выходе секции обрабатываются поочередно - зачастую методом циклической свертки.v Такие способы называются методами с перекрытием; в этом названии отралоется тот факт, что неперекрывающиеся секции в потоке входных данных приводят к перекрывающимся секциям в потоке выходных данных, а перекрывающиеся секции в потоке входных данных приводят к неперекрывающимся секциям в потоке выходных данных.

Работа показанного на рис. 1.5 авторегрессионного фильтра также может быть описана в терминах полиномиальной арифметики. Но если КИО-фильтр вычисляет произведение многочленов, то авторегрессионный фильтр выполняет деление многочленов. А именно, при фильтрации конечной последовательности в авторегрессионном фильтре (с нулевым начальным состоянием) на выходе фильтра формируется последовательность коэффициентов многочлена-част jro, получаемого при делении многочлена, коэффициенты которого равны компонентам входной последовательности, на многочлен, коэффициенты которого задаются весовыми множителями в отводах фильтра; к моменту завершения ввода входной последовательности содержимое фильтра равно коэффициентам многочлена-остатка от такого деления. Напомним, что авторегрессионный фильтр описывается равенством

= - £ ftiPj-i + oj,

где flj есть /-й символ на входе, а А; - весовой множитель в 1-м отводе фильтра. Определим многочлены

п-\ L

а (х) = Ц щx и Л (л:) = Ц ha

и запишем равенство

а(х) = Q,(x)h{x) г(х).

где Q (л:) и / (д:) обозначают соответственно частное и остаток в алгоритме деления многочленов. Тогда отсчет Pj на выхо.че фильтра равен в точности /-му коэффициенту многочлена-частного, а коэффициенты многочлена-остаТка г (х) будут записаны в самых левых разрядах регистра сдвига авторегрессионного фильтра после того, как на его вход будут поданы все п коэффициентов a делимого.

Другим очень важным в цифровой обработке сигналов видом вычисления является дискретное преобразование Фурье (с этих пор называемое в дальнейшем просто преобразованием Фурье). Пусть V = {Vi, i = О..... п - 1[ обозначает вектор с вещественными или комплексными компонентами. Преобразованием Фурье вектора v называется вектор V длины п с комплексными компонентами, задаваемыми равенствами

= и иЧ, А = О, ..., л - 1,

где CD = е- и / = i)-

Иногда это определение записывается в матричном виде

V = Tv.

Если раскрыть эту запись, то она принимает вид

1 0)2 -11

п-1

Если вектор V равен преобразованию Фурье вектора v, то вектор V можно вычислить по вектору V с помощью обратного преобразования Фурье, задаваемого равенством

п-1 fe=0

Доказательство этого факта дается следующими выкладками:

ft=0 4=0 (=0

Если / = i, то сумма по к, очевидно, равна я, а если / не равно i, то сумма приводится к виду

I ш- I-) 1 ш-<-1

Во всей книге буква / используется и для обозначения {/ -1 и в качестве индекса. Это не приводит, однако, ни к какой путанице.

Так как со = 1, то справа стоит нуль. Следовательно,

п-[ п-О

S ш-К, = S ti {пЬи) nv

t=0 1=0

где 6i; = 1 при i = / и 6;, = о в противном случае.

Между циклической сверткой и преобразованием Фурье имеется очень важная связь, которая известна как теорема о свертке и формулируется следующим образом. Вектор е равен циклической свертке векторов f и g,

1 = 0.....л - 1,

тогда и только тогда, когда их преобразования Фурье удовлетворяют равенствам

EtFtGt, к=.0 , л - 1.

Это утверждение вытекает из того, что

Поскольку e есть обратное преобразование Фурье от Е, то мы заключаем, что = GF-

Можно также определить двумерные преобразования Фурье, которые полезны при обработке двумерных таблиц данных, и многомерные преобразования Фурье, которые используются прн обработке многомерных массивов данных. Двумерное преобразование Фурье определяется равенствами

;г ir =0, л - 1,

1=о г=о к = и, .... л - 1,

где (О = е-2п/п и р = е- / .

1.5. История быстрых алгоритмов обработки сигналов

Историю быстрых алгоритмов обработки сигналов принято отсчитывать с момента, когда в 1965 г. Кули и Тьюки опубликовали свой быстрый алгоритм вычисления преобразования Фурье (БПФ-алгоритм), хотя на самом деле эта история началась намного