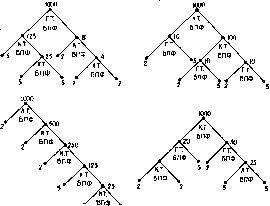Рис. 4.10. Некоторые способы построения 1000-точечного преобразования Фурье.

Фурье. На рис. 4.10 показано несколько способов разбиения 1000-точечного преобразования Фурье на преобразования меньшего объема. Каждый из способов содержит 2-точечный модуль три раза и 5-точечный модуль три раза. Но все процедуры существенно различны, так как малые модули используются в разной последовательности. Число умножений и сложений, чувствительность алгоритма к погрешностям вычислений и легкость реализации алгоритма различны.

4.4. Алгоритм Герцеля

Значение одной компоненты преобразования Фурье можно вычислить по правилу Горнера, дающему один из способов вычисления многочлена

о (х) = f -ix°- + v ,x- Н----+ ч,дг + о

в некоторой точке р. Правило Горнера, записанное в виде

№) = ( (( -iP + -2)P + y -3)P+ . + ci)P + o, требует п - 1 сложений и п - 1 умножений в поле элемента р. Еслн все различные степени элемента р вычислены заранее,

ТО правило Горнера не дает никаких преимуществ по сравнению с прямым вычислением. Преимущество правила Горнера состоит в том, что оно не требует предварительного вычисления и запоминания этих степеней.

Если р = ш*, то правило Горнера вычисляет к-ю компоненту преобразования Фурье посредством п - 1 комплексных умножений и п - 1 комплексных сложений. Более эффективным для этого вычисления является алгоритм Герцеля.

Алгоритм Герцеля представляет собой процедуру вычисления дискретного преобразования Фурье. Он позволяет уменьшить число необходимых умножений, но на очень малый множитель. Он не принадлежит к алгоритмам БПФ, так как его сложность по-прежнему пропорциональна п. Алгоритм Герцеля полезен в тех случаях, когда требуется вычислить малое число компонент преобразования Фурье, - как правило, не более чем log, п из п компонент. Так как БПФ-алгоритмы вычисляют все компоненты преобразования, то в этих случаях приходится выбрасывать ненужные компоненты.

Для вычисления одной компоненты преобразования Фурье

Vj = Е рассмотрим многочлен р (х) = (х - ш) (х - ю- ).

Он представляет собой многочлен наименьшей степени с вещественными коэффициентами, для которого элемент о)- является корнем. Это минимальный многочлен элемента т над полем вещественных чисел, и он равен

Пусть

p(x) = x -2cos (- к)х+1.

(Х)= Е VtX

и запишем

v(x) = р (X) Q(x)-tr (X).

Многочлен-частное Q (х) и многочлен-остаток г (х) могут быть найдены с помощью алгоритма деления многочленов. Тогда величина может быть вычислена по остатку согласно равенству

Vb = oK) = r(o) ), так как по построению величина р ( *) равна нулю. Большая часть работы приходится на деление многочленов. Если коэффициенты многочлена v (х) являются комплексными, то для его деления на многочлен р (х) требуется 2 (п - 2) вещественных умножений; если же коэффициенты многочлена v {х) являнхгся вещественными, тотребуется п - 2 вещественных умножений. Аналогично, необходимое число сложений в комплексном случае равно 4 (п - 2), а в вещественном 2 (п - 2).

146 ГлХ Быстрые алгоритмы дискретного преобразования Фурье vo, . . . , V -2, v i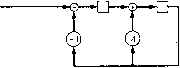

Замечания: Входные данные вещественные или комплексные.

.д=2соз-В*.

г (х) остается в регистре сдвнга после завершения деления

Для каждого своя цепь деления.

Vt = mf, + г,.

Рис. 4.11. Блок-схема алгоритма Герцеля.

Так как степень многочлена г (х) равна единице, то для вычисления г (ш*) требуется только одно комплексное умножение и одно комплексное сложение. Таким образом, при комплексном входе для вычисления одной выходной компоненты алгоритму Герцеля требуется 2/г - 1 вещественных умножений а An - 1 вещественных сложений.

Блок-схема алгоритма Герцеля показана на рис. 4.11. Эта схема имеет форму авторегрессионного фильтра. Это является следствием того, что схема деления многочленов имеет форму авторегрессионного фильтра. После ввода многочлена о (х) цепь на рис. 4.11 будет содержать остаток г (х) от деления многочлена Частное Q (х) интереса не представляет

V (х) на многочлен р {х я поэтому отбрасывается.

Чирп-алгоритм содержит п поточечных умножений v, на р- , циклическую свертку с Р в КИО-фильтре с п отводами и следующие за этим п поточечных умножений на р-*. Поэтому полное число операций по-прежнему имеет порядок п, так что чирп-алгоритм асимптотически не эффективнее прямого вычисления преобразования Фурье. Однако в некоторых приложениях он допускает более простую аппаратурную реализацию. Кроме того.

4.5. Вычисление преобразования Фурье с помощью свертки

Одним из эффективных способов вычисления дискретного преобразования Фурье

Vk = Ё (оЧ

является сведение к вычислению свертки. Это может показаться странным, так как мы уже знаем, что хорошим методом вычисления свертки является использование БПФ и теоремы о свертке. И на самом деле, возможно поэтому, многие годы рассматриваемые в данном разделе методы привлекали мало внимания. Сейчас, однако, стало понятно, что иногда выгодно вычислять преобразование Фурье сведением к вычислению свертки, а иногда, наоборот, выгоднее вычислять свертку через преобразование Фурье. Что еще удивительнее, иногда выгодно вычислять свертку через преобразование Фурье, реализуя при этом преобразование Фурье через алгоритм вычисления свертки, хотя и на длине, отличной от. исходной.

Два различных способа перехода от преобразования Фурье к свертке дают чирп-алгоритм Блюстейна и алгоритм Рейдера для простых чисел (см. рис. 4.12). Алгоритм Блюстейна переводит п-точечное преобразование Фурье в п-точечную свертку и 2п дополнительных умножений. Алгоритм Рейдера переводит п-точечное преобразование Фурье в (п - 1)-точечную свертку, но только для простых чисел п.

Алгоритм Блюстейна менее полезен, но проще в описании, так что мы начнем с него. Он описывается равенством

v = p- sp - (r i).

где р равно квадратному корню из ш. В этом варианте преобразования Фурье производятся следующие вычисления:

Чирп-алгоритм Блюстейна

- Кт-фиятр (ГУ.

Qupn

Qupn

Алгоритм Рейдера для простой длины Ялино п преобразования яблявтся простым <4ислом ИспальзоВагги, я - примитивный Эйвмвнт поля OF(n)

{1, 2, 3----, Л - 1) = lir, т.....mod /1)

n = K. = 0 + ui *: = 0.....n - 1/

1=0 i=o

( = 0.....n - 1

Перешанов/к

КИО-фильтр с Хп-Пвтеодами

Обратная перестановка

Сумма

Рис. 4.12. Сведение преобразования Фурье к свертке.

можно переписать, заменив индексы ( и k соответствующими степенями элемента я. Индексы i и к принимают и нулевые значения; эти компоненты входного и выходного векторов удобнее рассматривать отдельно. Тогда

1.....л = 1.

Пусть г (i) обозначает единственное для каждого i от 1 до л - I целое число, такое что в поле QF(n) выполняется равенство л (О = 1. функция г (<) является отображением множества jl, 2.....л - Ij на множество 1, 2, л - 1; она задает перестановку на множестве jl, 2.....п-\\. Тогда К можно записать в следующем виде:

Так как г (i) задает перестановку, то можно положить I = г (к) и / = л - 1 - г (i) и выбрать / в качестве индекса суммирова-HHHt это дает

прямое вычисление свертки можно заменить рассмотренными в гл. 3 алгоритмами быстрой свертки.

Алгоритм Блюстейна содержит 2/г умножений и свертку длины п. Более предпочтителен следующий алгоритм - алгоритм Рейдера, - так как он не содержит Чп дополнительных умножений. Алгоритм Рейдера содержит только некоторые операции по переиндексации входных данных и циклическую свертке, длина которой теперь уже равна п - 1.

Алгоритм Рейдера можно использовать для вычисления преобразования Фурье в любом поле f, если только длина преобразования п является простым числом. Так как п - простое число, то можно воспользоваться структурой поля GF (п) для переиндексации компонент входного вектора. Поле GF (п) не следует путать с полем F, в котором вычисляется преобразование Фурье.

Выберем примитивный элемент п простого поля GF (п). Тогда каждое не превосходящее п целое число можно однозначно записать в виде степени элемента п. Преобразование Фурье