Вход ВПФ: 75 точек

Вход БПФ: 25 точек

Отображение данных б таблицу 325

Отображение данных в таблицу 5*5

25-кратный вызоё

3-точечного преобразования

5-кратный Вызов 5-точечного преовразодания

Умножение таб ицыЗ& на и>-

Умножение таблицы J 5 на и}**

3-кратный вызов

25-точечного преобразования

5-к ратный вызов 5-точечного преобразования

Отображение табяицыЗ*25 в 75-точечный вектор

Отображение таблицы 5*5 в 25-точечный вектор

Выход бПФ: 75 точек

Выход 6ПФ: 25 точек

Вход вход

5-точечного лреабразованив 3-точечного преобразования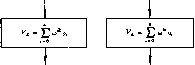

Выход Выход

5-точечного преобразования 3~точечного ореобразования

Рис. 4.4. Разбиение БПФ-алгоритма Кули-Тьюки на подпрограммы.

МОЖНО вычислять с помощью БПФ-алгоритма Кули-Тьюки.

На этом пути преобразование длины п = может быть пред-

ставлено в такой форме, в которой требуется выполнения пщ

комплексных умножений. На рис. 4.3 показан один из многих способов разбиения 75-точечного преобразования Фурье. Каждый из узлов этого рисунка можно представлять себе как обращение к подпрограмме. Если вычисления реализуются с помощью такого разбиения на подпрограммы, то один из способов организации программного вычисления показан на рис. 4,4. На самом нижнем уровне вычислений находятся 3-точечное и 5-точечное преобразования Фурье, выполняемые буквально. Позже мы построим малый БПФ-алгоритм Винограда, который можно использовать на этом уровне в качестве подпрограммы. Малые БПФ-алгоритмы Винограда представляют собой сильно оптимизированные процедуры вычисления преобразования Фурье для длин, являющихся простым числом или степенью простого числа.

4.2. Алгоритм Кули-Тьюки по малому основанию

Во многих приложениях, в которых используется алгоритм Кули-Тьюки, длина преобразования равна степени двух или четырех. Для построения БПФ-алгоритма длина 2 преобразования представляется в виде 2.2 -i или В этом случае говорят БПФ-алгоритме Кули-Тьюки по основанию два Аналогично, длина 4* преобразования разлагается в виде 4-4 -i или 4 -. 4, и тогда говорят о БПФ-алгоритме Кули-Тьюки по основанию четыре. Если в 2 -точечном алгоритме Кули-Тьюки по основанию два полагается л = 2 и л* = 2 -, то он называется БПФ-алгоритмом Кули-Тьюки по основанию два с прореживанием по времени. Используя тот факт, что р = о) /2 = -1 в этом случае уравнения, задающие БПФ, можно записать в следующем простом виде:

л/2-I п/2-l

i=0 (=0

n/2-1 n/2-I

= 0. л/2-I,

) Тернии по основанию два относится к факту записи индексов по основанию два. Компоненты данных могут быть представлены в любой системе счисления, в частности по основанию два.

л/2-I

V2k-= Е ( с + г+л/г)

(=0 л/2-1

Vlk-+I = Tl (Иг- 1Ч-г./2)мю .

к =0, .... п/2 - i.

Прореживание по частоте разбивает компоненты входного вектора на два подмножества, содержащие соответствеино первые /1/2 компонент и вторые п/2 компонент. Компоненты выходного вектора разбиваются на подмножество компонент с четными индексами и подмножество компонент с нечетными индексами.

Алгоритм с прореживанием по времени и алгоритм с прореживанием по частоте отличаются структурой и последовательностью вычислений, хотя имеют одно и то же число операций. Характеристики алгоритмов совпадают, но пользователь может предпо-. честь один из них из соображений реализации. Мы подробно рассмотрим только характеристики алгоритма с прореживанием по времени.

Алгоритм с прореживанием по времени сводит п-точечное преобразование Фурье к двум (п/2)-точечным преобразованиям Фурье с некоторыми дополнительными сложениями и умножениями. Часть из умножений представляют собой умножения на единицу или +/. Они тривиальны и не требуют действительного вычисления. Чтобы обойтись без тривиальных умножений в алгоритме, их следует обрабатывать отдельно. Иногда конструктор предпочитает включить в процедуру вычисления все умножения, даже тривиальные.

Алгоритм с прореживанием по времени работает рекурсивно, разбивая на каждом шаге п-точечное преобразование на два (/г/2)-точечных преобразования, которые, в свою очередь, разбиваются точно таким же образом. Из уравнений ясно видно, что число Ale ( ) комплексных умножений п-точечного БПФ удовлетворяет рекуррентному уравнению

М, (п) = 2М, (п/2) + п/2.

а число Л, (п) комплексных сложений удовлетворяет рекуррентному уравнению

А, (п) = 2А, {п/2) + п,

где п равно степени двойки. Решения этих уравнений даются равенствами

(п) = (л/2) loga л, (п) = п logj л.

Комплексные умножения можно реализовать алгоритмом с четырьмя вещественными умножениями и двумя вещественными сложениями. В этом случае характеристики БПФ по основанию два даютсг равенствами

Л1д (л) = 2п logj л, Л;, (л) = Зп logj л.

Альтернативный алгоритм выполнения комплексного умножения содержит три вещественных умножения и три вещественных сложения. В этом случае характеристики имеют вид

(п) = (3/2) п log, л, Л (л) = (7/2) л log, л.

Теперь предположим, что мы хотим построить алгоритм, в KofopoM выброшены все тривиальные умножения. Тогда полу-ченнЬте нами характеристики сложности алгоритма улучшатся. Тщательный анализ алгоритма показывает, что все умножения на самом внутреннем шаге алгоритма тривиальны и имеют вид умножений на (-1) для А = О, 1; все умножения на следующем шаге тривиальны и имеют вид умножений на /* для к - О, I, 2, 3; на последующих шагах число тривиальных умножений равно

п/4, л/8..... Следовательно, число комплексных умножений

равно

. МАп) = (л/2) (-3-flog, л).-1-2.

Используя для реализации комплексного умножения алгоритм с четырьмя вещественными умножениями и двумя вещественными сложениями, для БПФ-алгоритма по основанию два получаем

/И, (л) = 2п (-3 + log, л) + 8,

Ля (л) = Зл (-1 + log, л) + 4.

Используя для комплексного умножения алгоритм с тремя вещественными умножениями и тремя вещественными сложениями, получаем характеристики

/И (л) = (3/2) л (-3 -Ь log, л) + 6,

Л (л) = (1/2) п (-9 + 71og, л) -f- 6.

Еще немного можно улучшить алгоритм, если воспользоваться свойством симметрии тригонометрических функций. Заметим, что

(D-/S =(1 /) 2.

Прореживание по времени разбивает множество компонент входного вектора на два подмножества: множество компонент с четными индексами и множество компонент с нечетными индексами. Множество компонент выходного вектора разбивается при этом на мнйжество первых п/2 компонент и множество вторых п/2

компонент. -----------

г-точечный БПФ-алгоритм Кули-Тьюки по основанию два, в котором п = 2 - и п = 2, называется БПФ-алгоритмом Кули-Тьюки по основанию два с прореживанием по частоте. Уравнения БПФ в этом случае преобразуются к виду

Мв С ) = п (-7 + 2 1о Л (п) = Зп (-1 + loj

п) +4

Мя (п) = (1/2) п (-10 + 3 logj п) + 8. Лн (п) = (1/2) п. (-10 + 7 log, п) + 8.

Как мы видим, число вариантов алгоритма Кули-Тьюки весьма велико, но мы еще не перечислили все возможности; имеются и другие возможности улучшения алгоритма. На рис. 4.5 приведены характеристики некоторых БПФ-алгоритмов Кули- Тьюки. В таблицу помимо обычной формы алгоритма Кули- Тьюки включен БПФ-алгоритм Рейдера-Бреннера. Этот БПФ-алгоритм является модификацией алгоритма Кули-Тьюки, основанной на том, что с помощью переупорядочивания уравнений БПФ некоторые умножения на комплексные константы можно заменить умножением на вещественные константы.

Алгоритм Рейдера-Бреннера можно строить, исходя из уравнений для алгоритма с прореживанием по времени, но мы предпочитаем отталкиваться от уравнений для алгоритма с прореживанием по частоте:

v = s(f,-f tii+ )u> ,

k = 0,

1112-1

S (Ui - В(+ /2)шй) . (=0

n/2 - 1,

Определим рабочий вектор a равенствами

О, 1

I (vi - о,+ ,2)/[2/ Sin (2ni/n)l, i

a положим

n/2-1

Так как

fi/2-! nl2-\

A = 0,

1) =

= 0, = 1,

/1/2-1.

пП- 1,

i)ai2jSin(2ni J) = E (Wi - И(-)-п/2) 0) ,

- 5 Й s s

* ° S I E

2 S S

Ю K} -чг

(N <0 2

о u2

п. о

с -Ч s

о * a

ills 5

! 5S

Умножение на эту комплексную константу требует всего двух вещественных умножений и двух вещественных сложений. Таких умножений на щагах 3, 4, ... алгоритм содержит соответственно n/i, п/8, .... Их можно реализовать с помощью специальной процедуры умножения. При этом в зависимости от выбранной реализации комплексного умножения характеристики алгоритма будут даваться равенствами