б. Предположим, что допускается разложение многочлена над полем комплексных рациональных чисел, т, е. чисел вида а + /&, где а и й - ради-

/ ональные числа. Сколько теперь потребуется комплексных умножений, если в качестве модулей допускаются многочлены, имеющие числа 1, ±j в качестве коэффициентов? {Замечание: теперь комплексные числа считаются внутренними переменными и умножение на / не считается умно--жением.)

в. Имеет ли алгоритм (б) преимущества перед алгоритмом (а)? (Указание: рассмотреть, является лн циклическая свертка вещественной или комплексной.)

3.9. Выписать всю последовательность равенств вычисления линейной (4 X X 3)-сверткн по алгоритму Винограда, основанному на многочлене

т(х)=х{х-\- \){х-\)1х-\- 1).

3.10. Для представления в ЭВМ чисел с двойной точностью можно использовать запись числа в виде многочлена di-f do. Для такой записи чисел с двойной точностью выписать алгоритм умножения без округления, содержащий три умножения и четыре сложения чисел с одинарной точностью.

З.И. Используя алгоритм

-1-1 о -1 1-1 о -1 -1

I о о 1 о

и принцип трансформации), построить пять новых алгоритмов. Чем они интересны? \

3.12. Доказать, что для любого п > 1 в поле вещественных чисел лучший алгоритм вычисления /

S {х) = g ix) d (х) (modx + l) J

содержит больше умножений, чем лучший алгоритм вычвслейия s{x) = g (X) d (х) (mod л - l).

3.13. Найти такие целые числа п и л, что л < п, но п-точечная циклическая свертка требует большего числа умножений, чем л-точечная циклическая свертка.

З.И. Используя знание быстрых алгоритмов свертки, построить алгоритм 3-то-

чечного преобразования Фурье, Vh= ft =0,1,2, содержащий

только два нетривиальных вещественных умножения.

3.15. Построить алгоритмы для следующих вычислений;

а. s{x) = g (х) d (х) (mod х-\- х-\- 1).

б. S {х) = g {х) d (х) (modx).

в. S (х) = g ix) d (х) {mod х-\-х \).

3.16. а. Сколько вещественных умножений требует описанный в разд. 3.7 метод вычисления циклической комплексной свертки по модулю х - I?

б. Сколько комплексных умножений требуется по теореме Винограда о сложности для вычисления в поле комплексных чисел циклической свертки по модулю многочлена х - 1?

в. Объяснить все кажущиеся несоответствия.

См. теорему 9.2.1. - Прим. перед.

3.17. а. Предполагая, что все переменные являются независимыми вещественными величинами, доказать, что для вычисления двух комплексных произведений

е+ /7 = {а-\- jb) (с+ id), е+ = (а+/V) (c+/d), требуется выполнить шесть вещественных умножений.

б. Сколько потребуется умножений для одновременного вычисления следующих двух комплексных призведеиий;

е +1! ={а jb)(c+ id), e--\-if=ia-lb){c-\-idl7 В данном случае переменные повторяются.

в. Сколько потребуется умножений для одновременного вычисления следующих двух комплексных произведений:

е -\-if={a-\-jb){c-\-id). е + - (а - jb) {с - id)

3.18. а. Доказать, что вычисление

где все переменные являются комплексными, требует шести вещественных умножений.

б. Доказать, что вычисление

So + /So

где все переменные являются вещественными, также требует шести вещественных умножений. Таким образом, равенство нулю величин g и g[, как и в задаче а, не уменьшает числа необходимых умножений, в. Доказать, что вычисление

где все переменные являются комплексными, требует шести вещественных умножений.

г. Доказать, что вычисление -f /So

. 1 -f К .

L -}8l go .

где все переменные вещественны, требует четырех вещественных умножений. В этом случае равенство нулю переменных и g[ уменьшает необходимое число умножений. 3.19. Построить алгоритм 4-точечной циклической свертки над полем комплексных чисел. Сравнить этот алгоритм с алгоритмом, основанным на БПФ и теореме о свертке.

Замечания

Без какой-либо общей теории первые быстрые алгоритмы сверток коротких длин были описаны Агарвалом и Кули [1 ] (1977) в связи с развитыми ими многомерными гнездовыми методами. Описанный нами обший метод был предложен Виноградом [2] (1978). Примеры использования этого метода приведены в монографии [4] 1980 г. Виноград также доказал [3] (1977) теоремы о сложности рассмотренных алгоритмов свертки для полей комплексных и вещественных чисел.

Глава 4

БЫСТРЫЕ АЛГОРИТМЫ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ

Построение набора методов вычисления дискретного преобра- зования Фурье является одной из основных наших целей. Мы построим много таких методов, каждый из которых обладает различными преимуществами перед другими и каждый из которых наиболее пригоден при со(тветствующих обстоятельствах. Основных стратегий имеется две. Одна из них состоит в сведении дискретного преобразования Фурье к свертке, которая затем вычисляется описанными в предыдущей главе методами. Другая стратегия состоит в переходе от одномерного преобразования Фурье к двумерному, которое вычисляется проще. Хорошие алгоритмы вычисления дискретного преобразования Фурье для минимизации сложности вычислений используют обе эти стратегии.

Многие из изучаемых нами алгоритмов не зависят от частных особенностей поля, над которым определено дискретное преобразование Фурье. Поэтому мы часто будем опускать указание на конкретное поле и в этом случае алгоритм справедлив для любого поля. В других случаях, хотя общая идея алгоритма и не зависит от поля, над которым рассматривается дискретное преобразование Фурье, но некоторые детали алгоритма определяются спецификой поля. В этих случаях алгоритм должен строиться для конкретного интересующего нас поля. .

4.1. Алгоритм Кули-Тьюки

быстрого преобразования Фурье

Преобразование Фурье вектора v,

в том виде, как оно записано, требует порядка умножений и , сложений. Если число п является составным, то имеется не- , сколько способов перейти от этого преобразования Фурье к двумерному преобразованию или к чему-либо ему аналогичному. Это позволяет перевести вычисления в более эффективную форму

БПФ-алгоритм Кули-Тьюки (1965) п = пп

( = ( + ni i = Q, п - I;

(= О, .... л - 1. k = nk+ k k = О, n - 1;

6 = О, .... л - 1;

Число умножений я (л + л) + л

V,.,.

Рис. 4.1. БПФ-алгоритм Кули-Тьюки.

но за это приходится платить усложнением структуры. Алгоритмы подобного сорта известны под общим названием быстрого преобразования Фурье (БПФ). На рис. 4.1 приведена структура БПФ-алгоритма Кули-Тьюки, изучаемого в данном разделе. Рис. 4.1 интересно сравнить с рис. 4.8 из разд. 4.3, на котором приведена структура БПФ-алгоритма Гуда-Томаса.

Для построения БПФ-алгоритма Кули-Тьюки предположим, что п = nh . В выражении для преобразования Фурье сделаем следующую замену записи каждого индекса:

I = i

к = пк + к ,

Тогда

i = О.....п - 1,

Г = О, п. - 1,

= О.....п - 1,

к = О, - 1.

=11 Е а(г+ -п (

Раскроем скобки в показателе степени и положим <о = f и м = р. Так как порядок элемента m равен пп, то член в * = 1 можно опустить. Определим теперь двумерные переменные, которые тоже обозначим через v и V, задавая их равенствами

i =0, .... л - 1, = Г = 0, Л--1, к = 0.....п - 1,

Vk:k-=V .k+k;

А =0.....л - 1.

БдеАхут Р.

1 дш;и.рс1ниш преоиразования vypbc

Индексы fS точек на входе

отобратеньв

Ььшиедение

Индексы 2t тачки ив бгвд

Индексы 21 точки на выАодв

ПШЕЗШШШОВЛВВаШЕМВЕ]]

отобрамение

Рис. 4.2. Примеры

по методу Кули-Тьюки.

При ЭТОМ векторы входных и выходных данных преобразуются в двумерные массивы. Заметим, что компоненты преобразования V упорядочены в таблице не так, как компоненты сигнала v. Это упорядочивание известно под названием адресного тасования. В терминах двумерных переменных формула преобразуется к виду

2 yvr.

Хотя для.понимания эта формула более трудна, чем исходная, не число входящих в нее умножений и сложений существенно меньше. А именно, она содержит не более п (п + п + \) кол -плексиых умножений и п (п + п - 2) комплексных сложений вместо л комплексных умножений и комплексных сложений исходной формулы.

Визуально БПФ-алгоритм Кули-Тьюки выглядит как отображение двумерной таблицы в двумерную таблицу, как показано на рис. 4.2 для примеров с га = 15 и = 21. Вычисления состоят из -точечного дискретного преобразования Фурье каждого столбца, поэлементного умножения всех элементов таблицы соответственно на О) и -точечного дискретного преобразования Фурье каждой строки.

Чтобы для комплексного входного вектора v подсчитать полное число комплексных умножений и комплексных сложений, предположим, что внутреннее и внешнее преобразования Фурье вычисляются обычным способом, содержащим соответственно (n f а (л) комплексных умножений и п { - 1) и п (п - 1)

пр*овроао6ани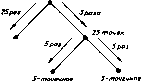

преобразование Фур1,е

преаВразоВаниа Фурье

Рис. 4.3. Структура 75-точечного БПФ-алгоритма Кули - Тьюки.

комплексных сложений. Каждое из этих преобразований Фурье используется п и п раз соответственно. Помимо этого имеется пл комплексных умножений на множители регулировки и*. Таким образом, полное число умножений, (п), и полное число сложений, (л), в данном случае равны

ММ) = п (nf + n (nf + пп = л (л -Ь 4- I), ЛДл) пп.п - 1) -Ьп л(л - 1) = п(л 4- л -2),

что и утверждалось ранее. Среди умножений имеются и тривиальные умножения на 1. Это происходит всякий раз, когда в множителе регулировки целые числа i или к в показателе обращаются Б нуль. При желании алгоритм можно перестроить так, чтобы выкинуть эти умножения; тогда число комплексных умножений станет равным

М, (л) = л (л -Ь л ) -f (л - 1) (л - 1) =

= ( -1)(л-Ьл)- (л-Ь1).

Внешнее и внутреннее преобразования Фурье в свою очередь могут быть вычислены с помощью быстрых алгоритмов, не обязательно с помощью БПФ-алгоритма Кули-Тьюки. Тогда для числа комплексных сложений и для числа комплексных умножений, входящих в БПФ-алгоритм Кули-Тьюки, получаем соотношения

Af, (л) = пМ, (л ) -f лМ, (л) -f л, А,{п) = пА,{п) + пА,(,п), где новые члены, стоящие в правых частях равенств, обозначают числа комплексных умножений и комплексных сложений, входящих соответственно в п-точечный и -точечный быстрые алгоритмы преобразования Фурье. Конечно, если п или п опять является составным числом, то меньшее преобразование опять 5