нений, но заведомо имеются случаи, в которых можно высказать диаметрально противоположную точку зрения. Большие цифровые процессоры часто сами создают потребность в разработке быстрых алгоритмов, так как размерность решаемых на ннх задач растет. Будет ли процессорное время алгоритма, предназначенного для решения некоторой задачи, пропорционально rf- или и, несущественно при п, равном 3 или 4, но при , равном 1000, это становится критичным.

Рассматриваемые нами быстрые алгоритмы связаны с цифровой обработкой сигналов, и ихприложения столь же широки, сколь и приложения самой цифровой обработки сигналов. Теперь, когда стало практичным разрабатывать изощренный алгоритм цифровой обработки сигналов, который может быть реализован конструктивно посредством одного чипа, хотелось бы иметь возможность выбрать такой алгоритм, который оптимизирует характеристики этого чипа. Но для больших чипов это невозможно сделать без достаточно развитой теории. В своем полном объеме такая теория существенно выходит за рамки включенного в данную книгу материала. Чтобы учесть все аспекты сложности, надо рассматривать и такие продвинутые разделы теории логических схем и архитектуры компьютеров, как параллельное или конвейерное исполнение.

Для оценки алгоритма обычно используют число необходимых умножений и сложений. Эти вычислительные характеристики почти исчерпывают сложность устройства на уровне алгоритма. На более низком уровне оно оценивается площадью чипа или числом логических элементов на нем и временем, необходимым для проведения вычислений. Часто в качестве критерия качества схемы используется произведение времени на площадь. Мы не будем пытаться оценивать характеристики на этом уровне, так как это выходит за рамки задач конструктора алгоритмов. - Актуальность рассматриваемых в данной книге вопросов нельзя оценить без понимания масштабов будущих приложений цифровой обработки сигналов. В настоящее время мы не можем угадать даже размеры таких систем, но достаточно просто можно предвидеть приложения, в которых объем необходимых вычислений будет на несколько порядков больше, чем тот объем, обработку которого может обеспечить современная технология.

Системы звуковой локации в последнее десятилетие стали почти полностью цифровыми. Хотя полоса частот, в которой они работают, равна всего нескольким килогерцам, эти системы выполняют десятки миллионов или сотни миллионов умножений в секунду и еще больше сложений. Такие системы уже сейчас нуждаются в мощном цифровом оборудовании, и стали обычными проекты, требующие еще более мощной цифровой техники.

Радиолокационные системы тоже становятся цифровы.ми, но многие важные функции по-прежнему реализуются традиционной микроволновой или аналоговой схемотехникой. Для того чтобы увидеть колоссальные потенциальные возможности использования цифровой обработки сигналов в радиолокации, достаточно отме тить, что радиолокационные системы в принципе очень nc-.v жи на системы звуковой локации, отличаясь от них тем, что испо.изу емая полоса частот в 1000 или более раз больше.

Цифровая обработка сейсмической информации является глав ным методом разведки земных недр, в частности одним из важнейших методов поиска залежей нефти. Обработкой больших пакетоп лент данных занято все процессорное время многих компьютеров, но многие вычисления остаются невыполненными.

Компьютерная томография представляет собой широко используемый ныне способ объемного синтеза изображений внутренних органов человека с помощью множественных проекций, получае мых при просвечивании рентгеновскими лучами. Разрабатываются алгоритмы, позволяющие существенно снизить дозы облучения, но требования к цифровой обработке намного превосходят все практически приемлемые в настоящее время. Изучаются и другие способы получения изображений для медицинской диагностики, в том числе о помощью ультразвука, ядерного .магнитного резонанса или радиоактивных изотопов.

Неразрушающий контроль качества подукцин, например отливок, возможен с помощью воссоздаваемых на компьютере изображений внутренних областей изделия по результатам эхолокации.

В принципе обработка сигналов может быть использована для улучшения качества плохих фотографий, смазанных движением камеры или расфокусировкой. Однако такая цифровая обработка требует большого объе.ма вычислений.

Обработка на цифровом процессоре спутниковых фотографий позволяет совместить несколько изображений или выделить особенности, или скомбинировать полученную на различных длинах волн информацию, или создать синтетический стереоскопический образ. Например, в метеорологических исследованиях можно создать подвижное трехмерное изображение облачного покрова, движущегося над поверхностью земли, используя для этого последовательность спутниковых фотографий, снятых с нескольких точек.

Можно указать и другие приложения быстрых алгоритмов для цифровой обработки сигналов, но уже приведенных достаточно для того, чтобы доказать, что потребность в них существует и продолжает расти.

Каждое из описанных приложений связано с большим количеством вычислений, структура которых, однако, чрезвычайно

прозрачна и сильно упорядочена. Кроме того, если для решения некоторой задачи уже создан жесткий модуль или подпрограмма, то они и будут постоянно использоваться для этой задачи. Имеет смысл затратить усилия на разработку добротной схемы, так как хорошие операционные характеристики намного важнее стоимости разработки.

1.3. Системы счисления для проведения вычислений

Во всей книге, говоря о сложности алгоритма, мы имеем в виду число умножений и сложений, поскольку эти операции выбраны в качестве единиц измерения сложности. Кто-то может захотеть пойти дальше и, чтобы подсчитать число необходимых битовых операций, поинтересоваться тем, как построено устройство умножения. Структура умножителя и сумматора существенно зависит от вида представления данных. Хотя вопросы, связанные с системами счисления, выходят за рамки данного курса, несколько слов во введении об этом сказать следует.

Возьмем крайний случай, полагая, что основная часть вычислений состоит из умножений. Тогда сложность можно понизить, записывая данные в логарифмическом виде. Сложение при этом станет более трудоемким, но если сложений не слишком много, то общий результат улучшится. Тем не менее, как правило, мы будем полагать, что входные данные записываются в одном из естественных видов - как вещественные, как комплексные или как целые числа.

В практической реализации процессоров для цифровой обработки сигналов имеются еще более тонкие вопросы; используются формы записи числа как с плавающей, так и с фиксированной точкой. Для большинства задач цифровой обработки вполне достаточной оказывается арифметика с фиксированной точкой и в этих случаях ее и надо выбрать из соображений экономичности. Этого положения не следует придерживаться слишком строго. Всегда есть соблазн избавиться от многих трудностей проектирования, перейдя к арифметике с плавающей точкой. Однако если чип или алгоритм предназначены для одного-единственного применения - например цифровой фильтр для цифровой радиосхемы массового выпуска, - то не стоимость разработки этого чипа играет основную роль; решающую роль играют эксплуатационные характеристики изделия и стоимость его тиражирования. Деньги, затраченные на облегчение работы конструктора, нельзя потратить на улучшение характеристик.

Неотрицательное целое число /, меньшее, чем q, в т-сим-вольной позиционной арифметике с фиксированной точкой по основанию q записывается в виде

/ = /о + кЯ + кЧ + + /m-i? *-. О < /i < 9.

Число / представляется т-последовательностью коэффициентов

(/ , /j..... 1). Имеется несколько способов учета знака

числа с фиксированной точкой; эти способы записи отрицательных чисел называются соответственно прямым кодом, дополнительным кодом и обратным кодом. При любом основании q правила такого представления одни и те же. В двоичном случае, ? = 2, дополнительный и обратный коды иногда называются соответственно 2-дополнительным и 1-дополнительным.

Наиболее прост для понимания прямой код. Для записи знака числа в нем выделяется специальная позиция, которая называется знаковой и в которую записывается Ь, если число положительно, и 1, если число отрицательно. В процессе выполнения операций сложения и умножения знаковая позиция обрабатывается отдельно от значимых позиций. Часто предпочтение отдается дополнительному 1ли обратному кодам, поскольку они проще реализуются в жестком исполнении; сумматор просто складывает два числа, не делая различия между знаковой и значащими позициями. Как прямой, так и обратный коды приводят к двум разным записям нуля - положительной и отрицательной, которые следует полагать равными. В дополнительном коде нуль записывается однозначно.

В обратном коде изменение знака числа получается заменой каждой цифры /, включая и знаковую цифру, на q - 1 - /. Например, взятое с обратным знаком десятичное число -f62 (которое записывается как 062) равно в обратном коде 937, а взятое с обратным знаком двоичное число -fOU (которое записывается как ООН) равно в обратном коде 1100. Обратный код обладает тем свойством, что для умножения любого числа на минус один достаточно каждую цифру заменить ее дополнением до ? - 1.

В дополнительном коде изменение знака каждого числа получается прибавлением единицы к записи этого числа в обратном коде. По определению минус нуль равен нулю. При таком соглашении взятое с обратным знаком десятичное число -f62, которое записывалось как 062, равно в дополнительном коде 938, а взятое с обратным знаком дв01чное число +011, которое записывалось как ООП, равно в дополнительном коде 1101.

1) в стандартной позиционной записи наиболее значимая цифра располагается не справа а слева, так что число записывается в виде /т-з (1. /о1- - Прим. перее.

1.4. Цифровая обработка сигналов

Наиболее важной задачей цифровой обработки сигналов является задача фильтрации длинной последовательности чисел, а наиболее важным устройством - цифровой фильтр. Как прави.ю, длина последовательности данных заранее неизвестна и является столь большой, что ее можно полагать при обработке бесконечной. Числа, составляющие последовательность, являются обычно либо вещественными, либо комплексными, но нам предстоит работать и с другими видами чисел. Цифровой фильтр представляет собой устройство, формирующее новую числовую последовательность, называемую выходной последовательностью, по заданной последовательности, которая теперь называется входной последовательностью. Широко используемые фильтры можно строить из эле-метов, схемы которых приведены на рис. 1.2 и которые называются разрядами регистра сдвига, сумматорами, умножителями на скаляр и умножителями. Разряд регистра сдвига содержит одно число, которое поступает на его выход. В дискретные моменты времени, именуемые тактами, разряд регистра сдвига замещает содержащееся в нем число числом, поступающим на его вход, отбрасывая предыдущее содержимое. Как показано на рис. 1.3, регистр сдвига представляет собой несколько соединенных в цепь разрядов регистра сдвига. Регистр сдвига называется также линией задержки.

Мы будем рассматривать два наиболее важных типа регистров сдвига, известных под названием фильтра с конечным импульс-ны.ч откликом (КИО-фильтр) и авторегрессионного фильтра. КИО-фильтр, как показано на рис. 1.4, представляет собой просто линию задержки с отводами, в которых выход каждого разряда умножается на фиксированную константу, а результаты складываются вместе. Как показано на рис. 1.5, авторегрессионный фильтр также является линией задержки с отводами, но с обратной связью, соединяющей выход со входом. Выходная последовательность КИО-фильтра равна линейной свертке входной последовательности и последовательности, описываемой весовыми множителями в отводах фильтра.

Линейная свертка является едва ли не самой общей вычислительной задачей цифровой обработки сигналов, и большую долю времени мы потратим на исследование вопроса ее эффективной реализации. Еще больше времени мы уделим методам эффективного вычисления циклической свертки. Это может показаться странным, так как в приложениях циклическая свертка возникает естественным образом не столь уж часто. Наше внимание к циклической свертке обусловлено тем, что для ее вычисления имеется много хороших алгоритмов. Это позволяет разработать быстрые методы вычисления очень длинных линейных сверток, связывая вместе много циклических сверток.

Разрид регистра сдвига

Умножитель на константу

Рис. 1.2, Элементы схем.

Сумматор

. Умиожитвдь

Рис. t .3. Регистр сдвнга.

----1*!. Ji.do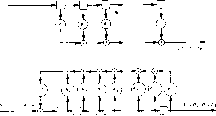

Рис. 1.4. КЛб-фильтр,

р. - - Б+

Рис. 1.5. Авторегрессивный фильтр.

Для заданных двух последовательностей - последовательности данных

d = di, ( = 0.....И-Х]

и последовательности фильтра

g = igi. i = 0.....lb

где iV -- длина блока данных и L - длина фильтра, линейной сверткой называется новая последовательность

S = Si, 1 = 0.....L + ЛГ - 2),

элементы которой определяются равенствами

= sfii-ft4, <=0.....L + W-2,